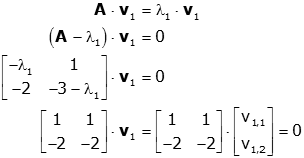
Eigenvalues & Eigenvectors Assignment Help

Eigenvalues & Eigenvectors

Order Instructions:

Hi Admin,

Please send me the answers by 28th June.

Thanks,
Customer

SAMPLE ANSWER

Eigenvalues & Eigenvectors

Problem 1

The matrix has eigenvalues1=3 and 2=−2. Let’s find the eigenvectors corresponding to 1=3. Let v=v2v1. Then(A−3I)v=0 gives us

2−3−1−4−1−3v1v2=00 from which we obtain the duplicate equations

−v1−4v2−v1−4v2=0

If we let v2=t, thenv1=−4t. All eigenvectors corresponding to1=3are multiples of1−4 and thus the eigenspace corresponding to1=3is given by the span of1−4. That is,1−4is a basis of the eigenspace corresponding to 1=3.

Repeating this process with 2=−2, we find that

4v1−4V2−v1+v2=0

If we let v2=t then v1=t as well. Thus, an eigenvector corresponding to2=−2 is 11 and the eigenspace corresponding to 2=−2 is given by the span of11. 11is a basis for the eigenspace corresponding to 2=−2.

Problem 3

Problem 5

Problem 14

Problem 22

Problem 25

Matrices A₂ and A₃ cannot be diagonized because for a square matrix A, wherever A is similar to diagonal matrix then the matrix is diagonizable.

Problem 15-24: Eigenvalues & Eigenvectors Matrices  

Problem 15

Since all entries are ≥ 0 and each column sums to 1, this A is a Markov matrix. Thus we know that λ1 = 1 is an eigenvalue. Since tr(A) = λ1 + λ2 = 3/2, we conclude λ2 = 1/2 is another eigenvalue. We diagonalize it using the matrix S of eigenvectors:

= → =

This last matrix product equals

Problem 19

1. False
2. True
3. True
4. False

References

Bhatti, M. A. (2012). Practical Optimization Methods with Mathematica Applications. New York, NY: Springer.

Edwards, C. H., & David E. Penney, D. E. (2009). Differential Equations: Computing and Modeling. Upper Saddle River, CA: Pearson Education, Inc.

Shores, T. S. (2007). Applied linear algebra and matrix analysis. New York, NY: Springer Science+Business Media, LLC.

Strang, G. (2003). Introduction to linear algebra. Wellesley, MA:  Wellesley-Cambridge Press

Strang, G. (2006). Linear algebra and its applications. Belmont, CA:  Thomson, Brooks/Cole Publishers.

Strang, G. (2009). Eigenvalues and Eigenvectors. Boston, MA: Lord Foundation of Massachusetts.

Zhang, F. (2009). Linear Algebra: Challenging Problems for Students, Baltimore, MA: The Johns Hopkins University Press.http://nsuworks.nova.edu/cnso_math_facbooks/3/

We can write this or a similar paper for you! Simply fill the order form!