Linear programming Paper Available

Linear programming

Linear programming

Order Instructions:

Just need to finish 4 simple question of linear programming of max/min problem.
you need to use excel (solver) in order to finish this.

ps i need to send you the question and some of the tut which similar to the assignment.

SAMPLE ANSWER

QUESTION 1

Let:

X₁ = number of large aircrafts

X₂ = number of medium aircrafts

X₃ = number of small aircrafts

Max z: 8×1 + 5×2 + 2×3

Purchasing LP model: 8×1 + 5×2 + 2×3  120

Number of aircrafts serviced

Capacity of aircrafts in tone-miles

Fixed operating costs:

The Excel solver screenshot:

QUESTION 2

Max:

St.LP with optimal solutions

Value of objective function

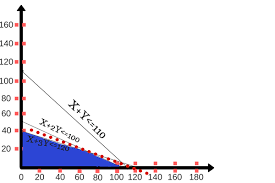
QUESTION 3

Let x₁ = Number of beds to produce

And x₂ = Number of desks to produce

The LP model for the problem is:

Max z: 30x₁ + 40x₂

Subject to: 6x₁ + 4x₂  36

4x₁ + 8x₂  40

x₁, x₂  0

QUESTION 4              

 

1. Because values of zero (0) in the “Allowable Increase” or “Allowable Decrease” columns for the Changing Cells indicate that an alternate optimal solution exists.

Initial R.H.S. = 15

Increased R.H.S. = 20

Allowable Increase = 45

This mainly because increasing the RHS value would definitely lead to increased optimal function value within the feasible region on basis of the allowable increase value provided.

6. 25.

Initial R.H.S. = 15

Decreased R.H.S. = 12

Allowable Decrease = 5

This mainly because decreasing the RHS value would definitely lead to decreased optimal function value within the feasible region on basis of the allowable decrease value provided.

Initial R.H.S. = 20

Increased R.H.S. = 32

Allowable Increase = 10

This mainly because increasing the RHS value would definitely lead to increased optimal function value within the feasible region on basis of the allowable increase value provided.

1. This is due to the fact that there would be an reduction in resources utilization leading to increased productivity.

	x1	const 1	const 2
	0	8	5
	1	6	4
	2	4	3
	3	1	1

References

Anderson D., Sweeney D., & Williams T (2007). An Introduction to Management Science. London: West Publisher.

Arsham H. (2007). An Artificial-Free Simplex Algorithm for General LP Models, Mathematical and Computer Modelling, 25(1), 107-123.

Arsham H. (2012). Foundation of Linear Programming: A Managerial Perspective from Solving System of Inequalities to Software Implementation, International Journal of Strategic Decision Sciences, 3(3), 40-60.

Chvatal, V. (2013). Linear Programming. New York, NY: W. H. Freeman and Company.

Lawrence J., Jr., & Pasternack, B. (2012). Applied Management Science: Modeling, Spreadsheet Analysis, and Communication for Decision Making. Hoboken, NJ: John Wiley and Sons.

Roos C., Terlaky, T. & Vial, J. (2009). Theory and Algorithms for Linear Optimization: An Interior Point Approach. Hoboken, NJ: John Wiley & Sons.

Shenoy G.V. (2010). Linear Programming: Methods and Applications. Hoboken, NJ: John Wiley & Sons.

We can write this or a similar paper for you! Simply fill the order form!