Triangular Factors and Row Exchanges
Order Instructions:
Please don’t put any pictures into the
coursework.
SAMPLE ANSWER
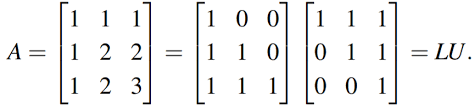
1.5. Triangular Factors and Row Exchanges
Question 1
Upper triangular matrix is non-singular when no entry on the main diagonal is zero.
Question 2
Solution:
Hence elimination will subtract 4 times row 2 from row 3.
Looking at the U matrix, we see the pivots along the diagonal of the matrix:
To find out if a row exchange will be needed or not, first we determine A
After carrying the first elimination, we get:
Hence, there would not be a need for a row exchange.
Question 3
Question 7
Question 13
Question 23
1.6. Inverses and Transposes
Question 1
Question 2
- When is applied to a matrix A its effect on A is to replace the first row of by the 3rd row of, the 3rd row of, and to replace the 3rd row by the first row at the same time. As an example. Hence to reverse this effect, we need to perform the same operation again, i.e. replace the 1st row with the 3rd row and replaced the 3rd row by the 1st row, this is P1
Hence,
Therefore,
Is an indication to replace 1st row by the 3rd row and to replace the 2nd row by the 1st row, and to replace the 2nd row by the 3rd row. For example; hence, in order to reverse it, we need to replace the 1st row by the 2nd row, and to replace the 2nd row by the 3rd row and to replace the 3rd row by the 1st row at the same time.
Hence,
- In a permutation matrix P, each row will have at most one non-zero entry with value of 1. Consider the entry Pi, j = This entry will cause row i to be replaced by row j. Hence to reverse the effect, we need to replace row j by row i, or in other words, we need to have the entry (j, i) in the inverse matrix be 1. But this is the same as transposing P, since in a transposed matrix the entry (i, j) goes to (j, Hence. Now, where , are permutation matrices (in other words, each row of is all zeros, except for one entry with value of 1.)
Hence the entry C (i, i) will be 1 whenever A (i, j) = B (j, i) = 1, this is from the definition of matrix multiplication, element by element view, since:
For all entries except when the entry, and at the same time, but since is the transpose of P, then whenever then only when.
Hence this leads to with all other entries in C being zero, i.e.
Question 4
(a)
If A is invertible and AB = AC, then B = C is true.
Because;
This means that; IB = IC, and subsequently B = C
(b)
Suppose:
AC = AB; then:
0 = AB – AC = A (B-C)
If , Note that if we define
Then you can find by multiplying it out that:
Therefore, if we set we find that:
So for this choice of A, just pick any 2×2 matrix for B, and define C = D + B; and automatically, you will find that: AC = A (D + B) = AD + AB = 0 + AB = AB; but C is not = B.
Question 6
Start with the augmented matrix:
Then the only row on the left that doesn’t already look like the identity matrix is the second row; we just need subtract rows 1 and 3 from row 2, which gives:
Hence,
To find, start with the augmented matrix:
Replace the 1st row by half of itself and add half of the 1st row to the 2nd row:
Next, add a third of the second row to the first, add 2/3 the second row to the third, and multiply the second row by 2/3:
Finally, multiply the third row by 3/4, and then add 1/3 of the result to row 1 and add 2/3 of the result to row 2:
Thus,
To find, start with the augmented matrix:
First, switch rows 1 and 3:
Now, subtract row 2 from row 1 and subtract row 3 from row 2:
Thus,
Question 10
For the first choice of A, we write the augmented matrix [A I]:
Then subtracting two times row 1 from row 2 and subtracting three times row 3 from row 2 yields
Hence,
For the second choice of A, write the augmented matrix [A I]:
Subtracting row 1 from rows 2 and 3 yields:
In turn, subtracting row 2 from rows 1 and 3 yields:
Finally, subtracting row 3 from row 2 yields:
Hence,
Question 13
Question 17
- The inverse of a lower (upper) triangular matrix is still lower (upper) triangular. Multiplying lower (upper) triangular matrices gives a lower (upper) triangular matrix.
- The main diagonal of and are the same as those of and , so we have. By comparing the off-diagonals of, both matrices must be diagonal. , is invertible so.
Then
Question 18
To make the pivot actually occur at f, switch rows 1 and 3:
Now, subtract d/j times row 1 from row 2 and subtract a/f times row 1 from row 3; note:
If e = 0 then the 2nd row is all zeros, which means that there can’t be a pivot in that row. Thus, when A is invertible, it must be the case that e 0. Therefore, a pivot is in the 2nd column, and the entry below can be eliminated through subtraction of times on row 2 from row 3:
If A is to be invertible, it must be the case that c 0. Therefore, the conditions which ensure that A is invertible are:
Turning to B, the matrix becomes:
Then, in order to have a pivot in the 2nd row, it must be the case that
Or, equivalently,
On the other hand, if, so we can switch rows 1 and 2 to get
Then we can eliminate a by subtracting times row 1 from row 2 (note:
Again, if we are to have a pivot in the 2nd row, it must be the case that:
Or, equivalently,
Therefore, either
Question 22
Question 43
The 5 by 5 also has 1s on the diagonal and super-diagonal.
Review Exercises
Question 1.2
Question 1.4
Question 1.10
Has L = I and;
A = LU has U = A (pivots on the diagonal);
A = LDU has with 1s on the diagonal.
Question 1.17
Question 1.28
2 by 2; d = 0 not allowed;
d = 1, e = 1; then l = 1, f = 0 is not allowed.
Vector Spaces
Question 2
The answer is: (a), (b) and (e).
Question 3
is the x-axis; is the line through (1, 1); is ; is the line through (-2, 1, 0); is the point (0, 0) in ; the null space is .
Question 14
The subspaces of are itself, lines through (0, 0), and the point (0, 0).
The subspaces of are itself, three-dimensional planes , two-dimensional subspaces , one-dimensional lines through (0, 0, 0), and (0, 0, 0) alone indicate that the smallest subspace containing P and L is either P or .
Question 24
The extra column b enlarges the column space, unless b is already in that space,
Reference
Strang, G. (2013). Linear Algebra and its Applications, (4th ed.). New York, NY: McGraw-Hill Publishers.
We can write this or a similar paper for you! Simply fill the order form!




